ME 5310 Midterm Exam 10-21-97 Name: _________________________________

Closed book & notes. One 8.5x11" sheet of equations is permitted. Use this page as the cover sheet for your solution. Turn your equation sheet in with your solution. Use one side of the paper only. Work the problems in any order, but submit your answers in the order shown below. The problems are each worth (100)/6 points.

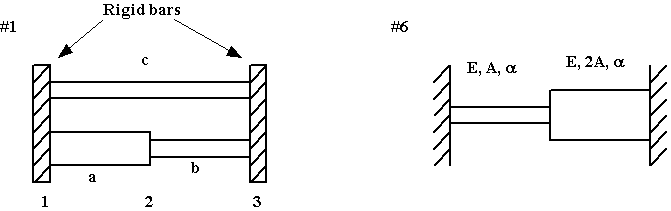
1. The rods shown below have numerical values for stiffness that can be represented as (AE/L) = a, b, c. (a) Use the concepts of equilibrium and compatibility to assemble the global stiffness matrix for the problem. (b) What set of nonsingular equations must be solved if R2 = P and u3 = 0.1? The rigid bars insure horizontal motion only.

2. At a point in an isotropic material in a state of plane strain we find that e x = 5x10-6, e y = -4.5x10-6, and g xy = 6x10-6. The material has elastic modulus E and Poisson's ratio n . Write out the equations needed to determine all of the stress components at this point.

3. The shape functions for the CST Triangle (area coordinates) and the Q4 Quad are given below. (a) Sketch the element and node numbering for each. (b) Use the shape functions to show that interelement compatibility is satisfied. (c) Why is interelement compatibility desirable?

4. A rod element has a uniformly distributed shear q lbs/in (N/m) applied to it. The shape function for the rod is given below. Derive the work equivalent nodal loadings that correspond to this distributed load.

5. (a) How many Gauss points are required to integrate exactly the stiffness matrix for a beam element? Explain.

(b) If you use displacement-based finite elements to solve a continuum problem (e.g., gear tooth stresses, thermal stresses in an engine block) are the calculated displacements too large or too small? Explain.

6. The rod structure is restrained between two walls and its temperature is increased by an amount equal to D T, what is the stress in the element on the left?

Solutions

Fall 97 Exam

1. [K] = [ a+c -a -c; -a a+b -b; -c -b b+c] (row1; row2; row3)

Assuming u1 = 0, P = (a+b)u2 -0.1*b

2. See class lecture

3. See class lectures

4. See class lecture

5. (a) not covered on midterm this year.

6. Not covered on midterm this year.

Fall 98 Exam

1. Using vertical and rotational displacements at the end of the beam, [K] = [13 -6; -6 4] (first row; second row)

P = 4 units of force.

2. See lecture

3. (a)& (b) See lecture

4. Max difference between node nos is 4 with numbering below.

6

2

10 9 5 1 3 7

4

8

5. See lecture