Some element stiffness matrices are easily developed in closed form. For example the closed form result for the simple truss element is

Evaluation of the stiffness matrix integral for the isoparametric formulation requires the use of a numerical integration process,such as the Gauss Quadrature method to evaluate the terms in the stiffness integral.

Consider the one-dimensional case in which we wish determine the area under curve f (x) shown in the figure.

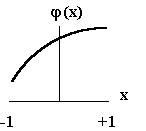
Suppose f (x) is a straight line. Then

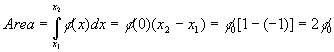
Where f ₀ is the value of the function at x = 0. This result may be represented as

Area

In other words, Integral = A constant (2 in this case) multiplying the Function evaluated at some point (the origin in this case).

For the example above, the function is linear, and only one function evaluation is needed to arrive at the value for the area under the curve. Suppose the function is a second order curve.

In this case we can show that the area under the curve can be found by evaluating the function at two points and multiplying those two function values by suitable weighting constants W₁ and W₂. Thus

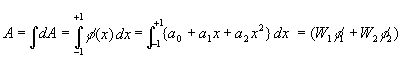
For a polynomial of arbitrary order, the area under the curve is given exactly by the expression

If the function is not a polynomial however, say f (x) = sin(x), the area under the curve can only be approximated by the result above.

Returning to the stiffness matrix integral, we wish to find

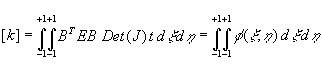
Where f (x ,h ) is a function in two variables to be integrated. If f (x ,h ) is a polynomial, the result can be obtained exactly. If not, the result will be approximate. Extrapolating from the one-dimensional case, we write

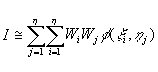
And use this approach to evaluate element stiffness matrices numerically at the time of formulation of each finite element problem.

The approach described above is used extensively to compute numerical values for the terms in element stiffness matrices.