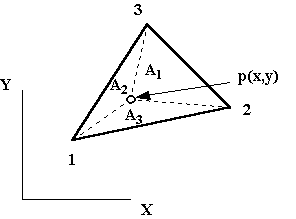
7-4 Area Coordinates
Introduction
Let p(x,y) be a point located arbitrarily in a triangular element. Nodes 1, 2, and 3 are located at the vertices of the triangle and numbered in a counter-clockwise order.
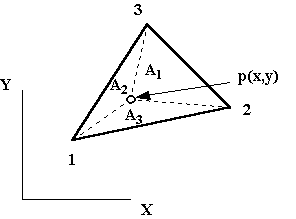
The point p divides the triangle into three subtriangles with areas A1, A2, and A3 opposite each node. An area coordinate, x , is defined as the ratio of the area of a subtriangle to the total area of the element.
![]()
The area of any triangle can be found by computing the determinate of a matrix containing the coordinate locations of the triangle vertices. Thus for A1
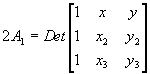
And
![]()
![]()
Collecting terms gives
![]()
![]()
Here
![]()
![]()
![]()
Thus 2A1 is a linear function of x and y, and the area coordinate becomes
![]()
Likewise
![]()
![]()
Area coordinates, linear functions of x and y, take on values between 0 and 1 as the point p moves within the element. For example, since x (x,y) is a function of x and y, when the point is located at node 1, x = x1, y = y1 and A1 = 1, A2 = A3 = 0. Thus
![]()
![]()
![]()
CST Development
The properties discussed above are very useful in developing shape functions and formulating stiffness matrices for triangular elements. The Constant Strain Triangle is used as an illustration.
In cartesian coordinates the displacement functions for the CST can be written as:
![]()
![]()
Here the a’s are determined from the boundary conditions on displacement at the nodes.
The element displacement functions can also be formulated in terms of the area coordinates as follows. For the CST let
![]()
![]()
Apply the displacement boundary conditions to u(x,y).
![]()
![]()
![]()
Thus
![]()
![]()
![]()
We see that the formulation with area coordinates makes determination of the unknown constants particularly easy. The displacement function for u(x,y) becomes
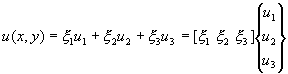
And for v(x,y)
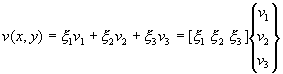
Since it is usual to order the element node displacement vector in the sequence u1, v1, u2, …, the CST shape function becomes.
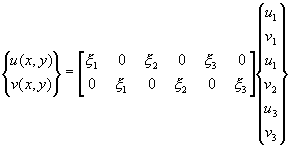
Where
![]()
We now use the strain-displacement relations to find expressions for the strains within the element. We use the chain rule of differentiation since the displacement functions are indirect functions of x and y.
![]()
Where
![]()
Thus
![]() and
and ![]()
The extensional strain in the x direction becomes
![]()
Where
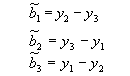
By the same kind of process we obtain
![]()
And
![]()
Collecting terms we obtain

The matrix B is
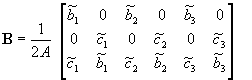
The CST stiffness matrix is found from
![]()
And the result is the same as that obtained by using cartesian coordinates in the formulation.
© 1999 Kent L. Lawrence