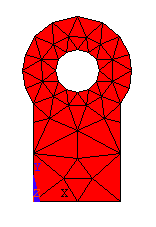
7-2 The Constant Strain Triangle (CST )
An element of triangular shape is easy to develop and can be used to model irregular boundaries. The three node triangular element was one of the first elements extensively used for continuum stress analysis.

The functions for displacements in the x and y coordinate directions can be described by polynomials as is shown next for u(x,y).
![]()
Here the a’s are constants to be found from the boundary conditions on displacement. Notations for the three node triangle are shown in the figure below.
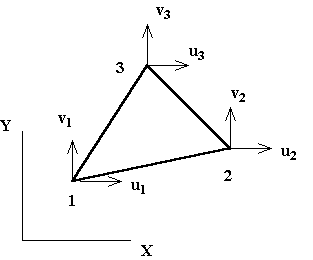
If we use only the linear terms from the general polynomial, the displacement function is approximated by
![]()
To evaluate the constants a1, a2, and a3, apply the displacement boundary conditions which relate the continuous displacement field u(x,y) to the specific displacements u1, u2, and u3 that occur at the corner nodes of the triangular element. (It is no accident that there are three unknown constants a and three specific node point displacement boundray conditions.) The nodes are numbered in a counter clockwise manner as shown.
These conditions are:
![]()
![]()
![]()
Or
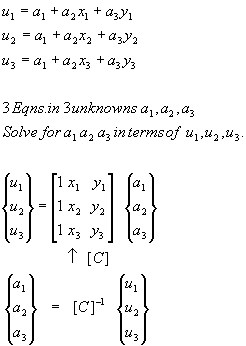
In the above, the matrix C contains the coordinates of the triangle corner nodes. Using C, the x direction displacement function is now expressed as:
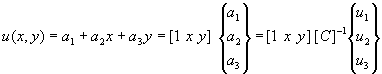
We may now find expressions for the extensional and shear strains within the element. The strain-displacement relations are given by
![]() ,
, ![]() ,
, ![]()
Using the displacement in the x coordinate to find the strain in x gives:
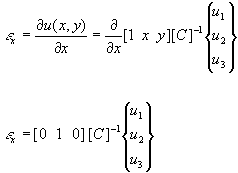
The development for displacement and strain in the y coordinate follows the same path as for the x coordinate. A linear displacement function is used as before.
![]()
Applying the displacement boundary conditions to the y displacement function gives:
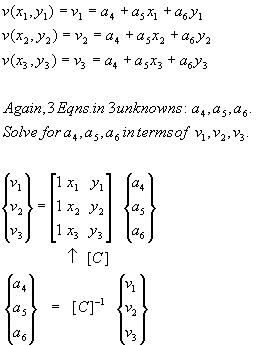
The linear strain in the y coordinate is given by the following.
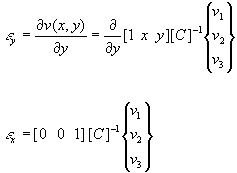
Using the u(x,y) and v(x,y) displacement functions, the shear strains within the element are given as:
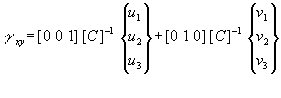
Displacement components are normally ordered so that all of the displacements at a node are grouped together when defining the element displacement vector d.
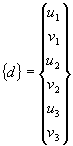
The matrix B(x,y) is then defined so as to express the relationship between the strains in the element and the element node point displacements.
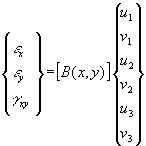
(B is a constant for the CST element, but is shown here as B(x,y) since it may be a function of x and y for other elements.)
The element stiffness matrix is given by
![]()
where E is the elasticity matrix for the stress-strain state under consideration. For triangular elements used in planar problems, E may describe a state of plane stress, plane strain, or a case in which the stress and strain state is symmetric with respect to a central axis (axisymmetric case).
The matrix C can be inverted symbolically using the coordinates of the triangle node points as known quantities.
![]()
![]()
Here A is the area of the triangle. The cofactors of C are given by:
cof11 = x2y3 – x3y2 cof12 = – (y3 – y2) cof13 = (x3 – x2) etc.
Using the determinate and the cofactors as found above, the strain-node point displacement expression becomes:
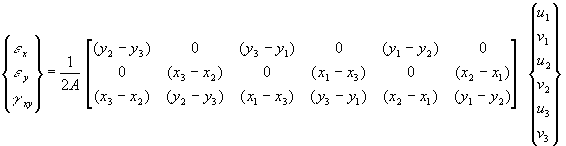
In the above, all entries in B are constants because of the assumption on the degree of the displacement polynomial used for u(x,y) and v(x,y). For elements with higher order polynomials, B = B(x,y).
The element stiffness matrix can now be found using the integral relationship
![]()
Since B is a constant for this element, the above reduces to
![]()
The product BTEB can be computed and a closed form expression obtained for the constant strain triangle stiffness matrix.
© 1999 Kent L. Lawrence