Isotropic Materials

It was Hooke's observation that for linearly-elastic, isotropic materials, normal strain is proportional to normal stress with Young's modulus or the elastic modulus, E, as the constant of proportionality. For a stress along the x direction

And Poisson observed that an extension along x is accompanied by contractions in the orthogonal directions y and z.

where Poisson's ratio n is the constant of proportionality. If a normal stress in the y direction is added to this, it would cause an extension in the y direction and proportional contractions in the x and z directions. For small deformation we can superpose the results.

Adding a third stress component in the z direction and rearranging terms gives generalized Hooke’s law for the normal components of stress and strain.

The shear strains are uncoupled from the normal strains and from each other for an isotropic material.

Here G is the shear modulus for the material, but only two elastic constants are needed to characterize an isotropic elastic material. Thus the shear modulus can expressed in terms of E and n , and G can be eliminated.

In the three-dimensional case there are six stress and six strain components. Referenced to a Cartesian coordinate system, x, y, z, the stress and strain vectors are written as follows.

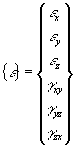
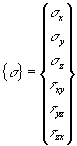
The relationships between strain and stress can be written as

where C is the compliance matrix of elastic constants relating strain and stress. Using the notations above.

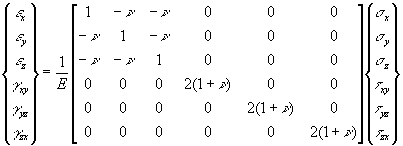
The inverse of this relationship is also of interest, that is, stresses written in terms of strains. Symbolically

where E = C^-1 is a matrix of elastic constants relating stresses to strains. Inverting the compliance relation gives the stress-strain relation for an isotropic material with six stress and strain components as follows.

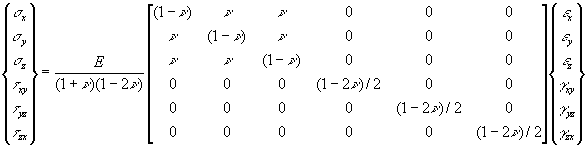
There are three important sub-cases of the general 3D stress/strain situation that occur frequently enough to be identified. These are a state of plane stress, a state of plane strain, and a case involving axisymmetric geometry and loading which causes axisymmetric stresses and strains. Some simplification of the generalzed Hooke's laws can be realized in each case.

Plane Stress

In a case of plane stress, one direction can be found that is free of normal stress and shear stress. If we orient the z-axis in this direction, we have

The generalized Hooke's law equation reduces to

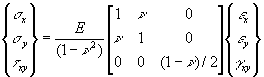
Plane Strain

In this case we have a direction along which the extensional strain is zero, and selecting the z axis as that direction, we havee _z = 0, and the extensional stress-strain relations may be combined as follows.

Use the last equation to solve for s _z and substitute the result into the other two equations. This gives

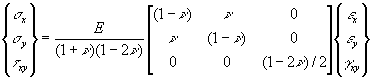
Axisymmetric Case

If the geometry, material properties, loading, and boundary conditions are symmetric with respect to an axis, it can be shown using symmetry arguments that while circumferencial stresses exist in the object, the shear stresses on a cicumferential plane are zero. Further, the stress state on any diametral plane is the same; meaning that the problem may be formulated and solved in two dimensions as long as the circumferential constraint is included in the analysis. In cylindrical coordinates r, q , z, the stress components are s _r , s _z , s q , and t _rz. Generalized Hooke's law for the axisymmetric case becomes

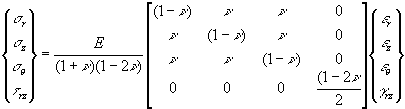
Anisotropic Materials

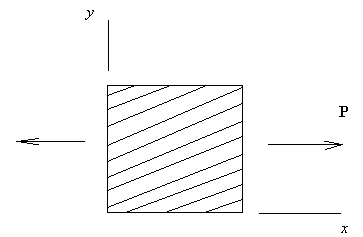
If a material is anisotropic, there is coupling between stress and strain that is not present in isotropic materials. For example, in the figure showing a coupon taken from a reinforced material (reinforced fiberglass, wood, reinforced concrete, etc.) note that a tensile stress causes an tensile strain and a shearing strain as the reinforcing fibers try to align themselves with the load.

For general anistropic materials, nonzero terms in the E matrix express this coupling between stress and strain components, and the symmetric matrix contains 21 nonzero terms in the general case.

Some simplification to this occurs for materials with three orthogonal planes of elastic symmetry. Such materials occur frequently in applications and are called orthotropic materials