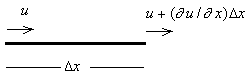
5-3 Strain - Displacement Relations

If a point moves with relative to another nearby point in an object, a strain occurs. Stated another way, a strain is caused when a gradient in the displacement field occurs in an object. An object that moves as a rigid body has no strain. Below we develop expressions for normal and shear strains in terms of the displacements within an object.

Normal Strain

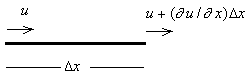
Consider a small element of material, D x, as shown in the figure. To account for a variation in the displacements in the x direction, the displacement at one point is represented by u(x), and the displacement of a nearby point is represented by u(x+D x) using the first two terms in a Taylor series. The left end of the element has a displacement u(x), and the right end moves an amount .

Defining engineering strain as change-in-length divided by original-length, gives the normal strain in the x directions as

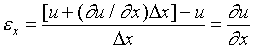
Using the same approach for the y and z normal strains gives

Here the displacements of all points within the object are described by functions u(x, y, z), v(x, y, z) and w(x, y, z) in the x, the y, and the z Cartesian directions, respectively.

Shear Strain

Shear strain is defined as the change in an angle that was originally a right angle before deformation occurred. In the figure, a + b constitute the shear strain for the element in the x-y plane as shown. For the small elastic deformations of interest to us, the angle in radians and its tangent are essentially the same. We compute the shear strain by finding the tangent of a and b using the gradients of the displacement functions u and v.

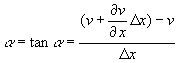or

By a similar argument we show that

Thus the shear that occurs between the x and y axis directions is given by

And for the other axes we have

Given a representation for the displacement fields, we can compute the strain components using the equations just developed.