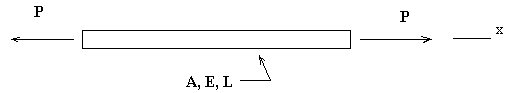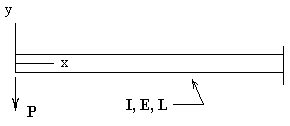Using a small element of material, D x D y D z, from a linear elastic body as shown in the figure, we can write the equations of equilibrium for the stress components acting on the faces of the element. Since the stresses change as one moves from point to point within the body, a variation in each stress term is considered using a first order Taylor series expansion. (For simplicity only the x normal and xy shear stresses are shown.)

Summing forces in the x direction gives:

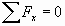
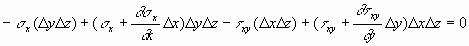
Which simplifies to the following.

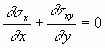
If there is an element force, X_b, in the x direction that is proportional to the volume (a ‘body force’), such the weight or an electromagnetic force, it must be added to the above. Writing the equation of equilibrium for the stresses in the y direction produces a similar result.

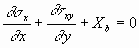
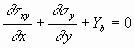
Considering a three-dimensional case in which stresses act in the x, y, and z directions gives the following set of equations of equilibrium.

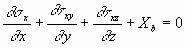
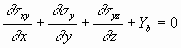
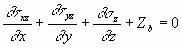
The correct stress distribution for a problem in solid mechanics must satisfy these equations of equilibrium.

Example 5-2-1 Consider an axially loaded, uniform rod.

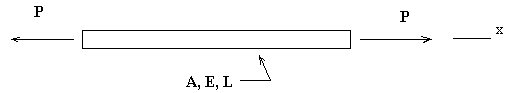
The axial stress is given by s _x = P/A ; all other stresses are zero, and you see by substitution into the above equations that equilibrium is satisfied.

Example 5-2-2 For pure bending of a beam by a moment M that does not vary along the length of the beam, the bending stress is given by s _x = -My/I , and all other stresses are zero. Again, the equilibrium equations are satisfied when s _x is substituted.

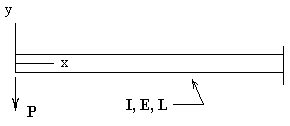
Example 5-2-3 For the end-loaded cantilever beam shown, the moment varies linearly along the length of the beam giving the following for the bending stress.

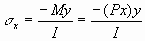
We can calculate the shear stress using element beam theory. In the following V is the shear force at position x, and Q is the first moment of the cross sectional area above the point y where the shear stress is to be found. If the beam cross section is rectangular with width b and height 2c, we obtain.

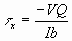
Where

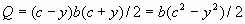
Thus

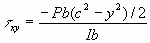
Substituting these two results into the first equation of equilibrium gives

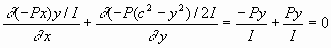
Since

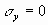and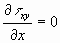

the second equation is satisfied automatically, and we observe that the stresses in an end-loaded cantilever beam as found from elementary beam analysis do satisfy the equations of equilibrium.