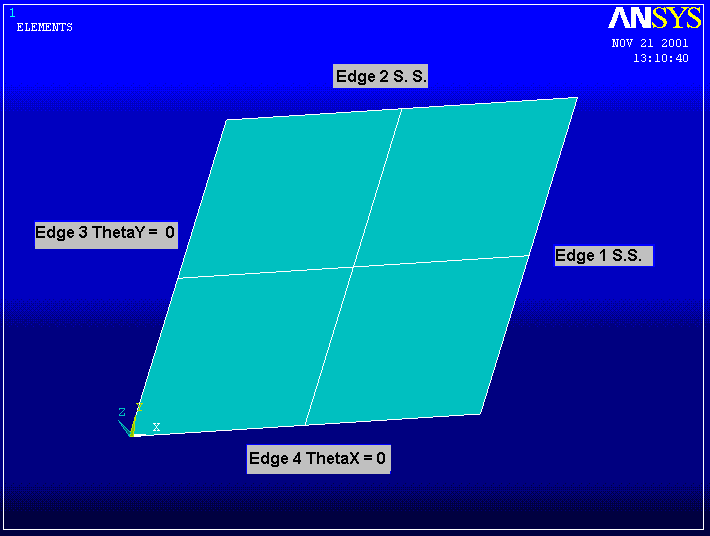
Deflection of a Simply Supported Plate with a Central Point Load - Consider a 10 inch x 10 inch steel plate that is 0

Deflection of a Simply Supported Plate with a Central Point Load - Consider a 10 inch x 10 inch steel plate that is 0.1 inch thick and has a 1.0 lbf force applied at its center. The plate is simply supported on all sides. Determine the deflection at the load point as a function of the number of elements used per side to model the plate.

ANSYS Solution

The plate has two planes of symmetry, so we model just one quadrant and apply appropriate boundary conditions. Use the ANSYS four node element shell63 for the model.

Start ANSYS and select the working directory for this problem

Select the element.

1. Preprocessor -> Element Type -> Add/Edit/Delete -> Add -> Shell -> Elastic 4 Node 63 -> Close

Specify the plate thickness

2. Preprocessor -> Real Constants -> Add/Edit/Delete . . . -> Add -> Shell Thickness at Node I Enter 0.1 -> OK -> Close

Get material properties for 304 steel.

3. Preprocessor ->Material Props -> Material Library -> Import Library . . . -> BIN -> Stl_AISI-304.BIN_MPL -> OK

Create a 5 inch x 5 inch area.

4. Preprocessor -> -Modeling --> Create -> Areas -> Rectangle -> By 2 Corners -> Enter 0.0, 0.0, 5.0, 5.0

Mesh the area with 2 elements per edge. First set the size controls so that 2 elements per edge are created.

5. Preprocessor -> Meshing -> Size Controls -> All Lines -> NDIV Number of element divisions -> Enter 2 -> OK.

6. Preprocessor -> Meshing ->Mesh -> Areas -> Free (Select the 5 x 5 square)

Apply boundary conditions and loads. Assume the global axis system is located at the center of the plate and that the simply supported edges are at x = 5 and y = 5. Edges 1 and 2 are Simply Supported. This means no displacement in the vertical direction and that the slope normal to the edge must be zero. Edges 3 and 4 are along lines of symmetry, and the plate must have a symmetric deformation shape across the lines of symmetry.

Edge 1

7. Preprocessor -> Loads -> Apply -> Displacements -> On Lines -> Select Edge 1 -> Set UZ = 0 -> OK Then repeat and set RotX = 0.

Edge 2

8. Preprocessor -> Loads -> Apply -> Displacements -> On Lines -> Select Edge 2 -> Set UZ = 0 -> OK Then repeat and set RotY = 0.

Edge 3

9. Preprocessor -> Loads -> Apply -> Displacements -> On Lines -> Select Edge 3 -> Set UX = 0 -> OK Then repeat and set RotY = 0.

Edge 4

10. Preprocessor -> Loads -> Apply -> Displacements -> On Lines -> Select Edge 4 -> Set UY = 0 -> OK Then repeat and set RotX = 0.

Apply one-quarter of the total load to the keypoint at the origin of coordinates.

11. Preprocessor -> Loads -> Apply -> Force/Moment -> Keypoints -> Select Keypoint at origin. For FZ enter -0.25 -> OK.

Perform solution

12. Solution -> Current LS -> OK

Post processing

13. General Postproc -> Plot Results -> Deformed Shape . . . -> Def + undeformed

Determine the deflection at the center of the plate.

14. General Postproc -> List -> Results -> Nodal Solution DOF solution -> All DOFs DOF

PRINT DOF NODAL SOLUTION PER NODE

***** POST1 NODAL DEGREE OF FREEDOM LISTING *****

LOAD STEP= 1 SUBSTEP= 1

TIME= 1.0000 LOAD CASE= 0

THE FOLLOWING DEGREE OF FREEDOM RESULTS ARE IN GLOBAL COORDINATES

NODE UX UY UZ ROTX ROTY ROTZ

1 0.0000 0.0000 -0.47295E-03 0.0000 0.0000 0.0000

2 0.0000 0.0000 0.0000 0.0000 -0.11886E-03 0.0000

3 0.0000 0.0000 -0.28975E-03 0.0000 -0.10641E-03 0.0000

4 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000

5 0.0000 0.0000 0.0000 0.0000 -0.80563E-04 0.0000

6 0.0000 0.0000 0.0000 0.11886E-03 0.0000 0.0000

7 0.0000 0.0000 0.0000 0.80563E-04 0.0000 0.0000

8 0.0000 0.0000 -0.28975E-03 0.10641E-03 0.0000 0.0000

9 0.0000 0.0000 -0.19383E-03 0.65232E-04-0.65232E-04 0.0000

MAXIMUM ABSOLUTE VALUES

NODE 0 0 1 6 2 0

VALUE 0.0000 0.0000 -0.47295E-03 0.11886E-03-0.11886E-03 0.0000

Note that the deflection at the center of the plate (node 1) is -0.47295E-03 inches.

The theoretical solution to this problem gives a deflection value of 0.452E-3 inches. Thus, our mesh is not fine enough to give an accurate deflection solution. As verification, plot the calculated von Mises Stress

15. General Postproc -> Plot Results -> Element Solu . . . -> Stress -> von Mises SEQV

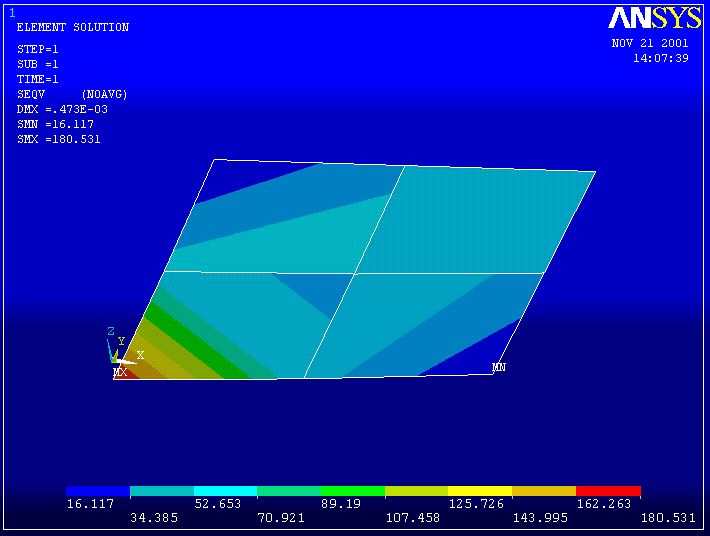
The discontinuities in stress contours indicate an inaccurate solution for this mesh and element. To improve the accuracy, clear the mesh (Preprocessor -> Meshing -> Clear -> Areas) and remesh with 4 elements per edge. Then repeat with 8 elements per edge. The deflection results are shown below.

Elements per edge Deflection

Elements per edge	Deflection
2	0.473E-3
4	0.461E-3
8	0.457E-3
Theory	0.452E-3

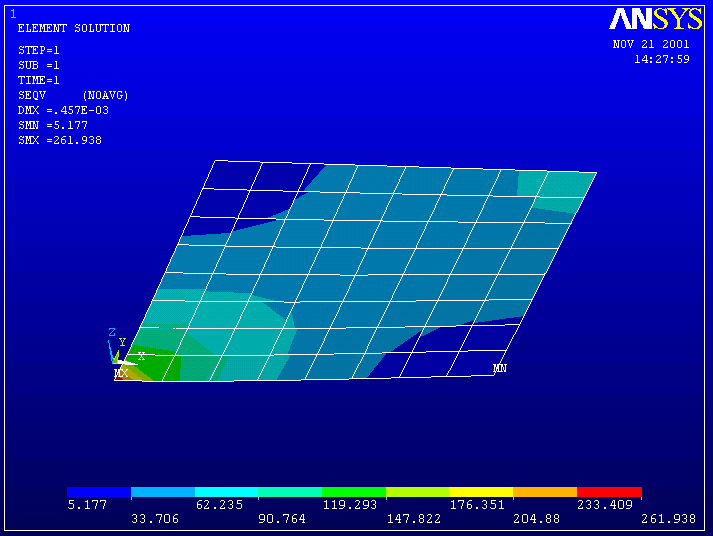
We observe that the last mesh produces deflection with an error of only 1.1 %. The von Mises stress plot for this case is shown below.

The stress contours are now much smoother in comparison with the first mesh. (Since the stresses are proportional to the spatial derivatives of the displacements, the stresses generally have greater error than the displacements.)

To obtain yet greater accuracy for this problem, increase the mesh density or switch to the eight node SHELL93 element, or do both.