Plane Stress example problem

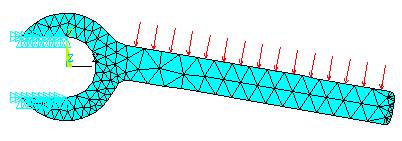
Given: The wrench shown is made of a steel with a yield strength of 45,000 psi. and is loaded with a pressure of 150 psi. along its handle as shown. It is 0.4 inches thick and about 7 inches in length.

Find: Determine if any yielding occurs because of this load.

Solution: The geometry was created in Pro/E, saved as an IGES file and imported into ANSYS 6.1. The plane2 6 node triangle element, plane stress with thickness option was used in the modeling.

Material properties were E = 3.e7 psi, nu = 0.3.

Boundary conditions ux = uy = 0 were applied along the lines where the wrench contacts the bolt.

The mesh was refined to eliminate element-solution stress contour discontinuities. The following plots of von Mises stress show a maximum value of 39,333 psi at the fillet radius on the underside of the wrench.

Data entered Interactively:

Element Type:

LIST ELEMENT TYPES FROM 1 TO 1 BY 1

ELEMENT TYPE 1 IS PLANE2 2-D 6-NODE TRI. STRUC. SOLID INOPR

KEYOPT(1-12)= 0 0 3 0 0 0 0 0 0 0 0 0 0

CURRENT NODAL DOF SET IS UX UY

TWO-DIMENSIONAL MODEL

Thickness:

LIST REAL SETS 1 TO 1 BY 1

REAL CONSTANT SET 1 ITEMS 1 TO 6

0.4000 0.0000 0.0000 0.0000 0.0000 0.0000

Material Properties:

EVALUATE MATERIAL PROPERTIES FOR MATERIALS 1 TO 1 IN INCREMENTS OF 1

MATERIAL NUMBER = 1 EVALUATED AT TEMPERATURE OF 0.0000

EX = 0.30000E+08

PRXY = 0.30000

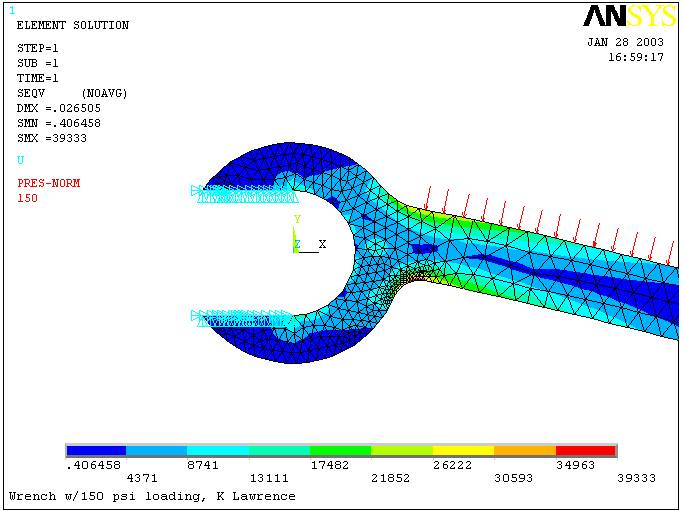
(Note: To properly document the model, the axis system, loads and boundary conditions are shown on this plot.)

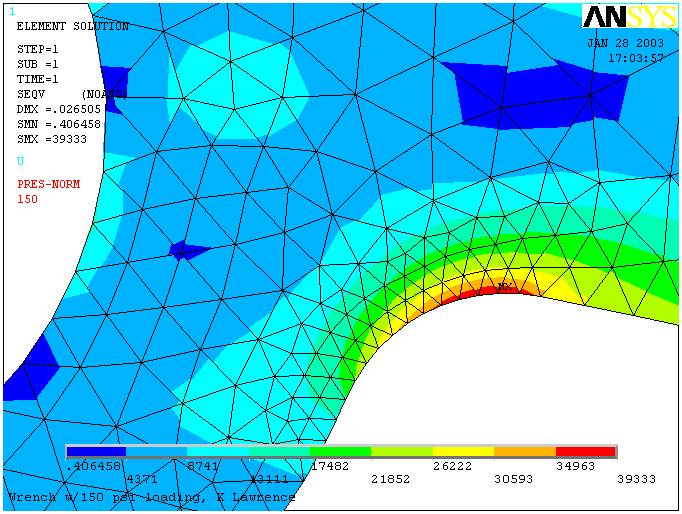
Results:

The maximum von Mises stress, SEQV = 39,333 psi, is less than the material yield strength of 45,000 psi, so no yielding is likely to occur.

(Note: In some cases it may be necessary to identify stresses or strains at critical elements and/or nodes, turn on element or node numbering and list the computed values at those locations as shown in ANSYS Tutorial Fig. 3-10. In the above we just used the contour plot legend.)