Cyclic Symmetry – The 3-D cylinder problem of Example 5.A can be solved with a much smaller model because of its innate symmetry. Any slice behaves just like any other slice. We illustrate this by solving the problem again working with a ten-degree slice (instead of 90 degrees) defined in global cylindrical coordinates.

1. Start ANSYS and establish jobname and working directory as usual.

The angular coordinate theta corresponds to a rotation about the Z axis.

3. In the Preprocessor create ten-degree wedge with 5 inch inner radius, 11 inch outer radius, and one inch height. Use Create > Volume > Partial Cylinder to do this.

4. Displacement Boundary conditions are applied to restrain motion in the Y direction on the X-Z face of the wedge.

Preprocessor > Loads > Apply > Displacement > On Areas Select the X-Z face and set UY = 0.

On the symmetric face of the wedge apply Symmetric Displacement conditions.

Preprocessor > Loads > Apply > Displacement > -Symmetry B.C. - On Areas Select the symmetric face OK. The 'S' in the figure below indicates a symmetric BC.

Apply a pressure of 1000 psi to the interior surface and restrain the lower surface of the wedge from motion in the Z direction.

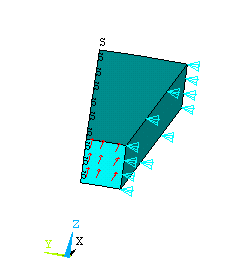
5. Select Solve > Current LS and Postprocessor > Plot the Element Solution SEQV to obtain the plot below. Notice that a smooth solution is obtained with much fewer elements than in the previous example.

The component stresses SX, SY, SZ, SXY, etc will be aligned with the global XYZ axis system and reflect the stress state shown on the X-Z face of the wedge.

 This approach is particularly useful for analysis of items with cyclic symmetry such as the flange shown in the figure below. The geometry, boundary conditions, loadings, and materials must be symmetric with respect to an axis of revolution. Then take a sector from the center of one hole to the center of the next. Or use a sector centered about a hole.